Two-DOF Damped Vibration System.

Hey everyone, welcome back to my blog. This time I am going to tour you through the two degree of freedom free damped vibration system with python implementation. So, lets deep dive into this article.

So, let me ask you a question,

What is 2-DOF damped vibration system?

Any guesses??? 

Nope?? Then, let's check what could be the answer....

A two-degree-of-freedom (2-DOF) free damped vibration system is formed from two masses with two spring and two dampers connected to it. For formulating equations of motion, it involves both the masses. The general representation of a 2-DOF free damped vibration system is as follows,

Consider,

• m1 and  m2 are the masses of first and second body (mass) respectively.
• c1 and c2 are the damping coefficients of the dampers connected to first and second body (mass) respectively.
• k1 and k2 are the stiffness coefficients of the springs connected to first and second body (mass) respectively.
• x1(t) and x2(t) are the displacements of first and second body (mass) respectively as a function of time, t. 
• v1 and v2 are the velocities of first and second body (mass) respectively as a function of time, t.
• a1 and a2 are the accelerations of first and second body (mass) respectively as a function of time, t. 

Figure 1: Spring-mass-damper system of 2 DOF system.

Differential Equations are very much helpful for modelling complex dynamic systems which are time dependent. So, we are going to use this incredible mathematical concept to model our 2-DOF freedom system as follows,

The equations can be written as system of second-order ordinary differential equations (ODEs).

For the first mass (m1),

For the second mass (m2),

Solving the above equations for given initial conditions, which are, x1(0), x2(0), v1(0), v2(0) and parameters m1, m2, k1, k2, c1 and c2 will give us time dependent displacements x1(t) and x2(t), and velocities v1(t) and v2(t) of both masses.

Now, it’s time for some python stuff, so prepare your fingers to hit some buttons!!

# Importing necessary libraries

import numpy as np

from scipy.integrate import odeint

import matplotlib.pyplot as plt

# Defining the system variables

mass1 = 3.0                # Mass of the first mass (kg)

mass2 = 1.0                # Mass of the second mass (kg)

stiffness1 = 30.0          # Spring constant of the first spring (N/m)

stiffness2 = 10.0          # Spring constant of the second spring (N/m)

dampingCoeff1 = 1.5  # Damping coefficient of the first damper (N*s/m)

dampingCoeff2 = 0.5  # Damping coefficient of the second damper (N*s/m)

# Initial conditions

displacement1_0 = 0.5                  # Initial displacement of mass 1 (m)

displacement 2_0 = 0.2                 # Initial displacement of mass 2 (m)

velo1_0 = 0.0                               # Initial velocity of mass 1 (m/s)

velo2_0 = 0.0                               # Initial velocity of mass 2 (m/s)

# Defining function for Ordinary Differential Equations of the 

# 2-DOF system

def TwoDOFsystem(state, time):

    displacement1, displacement2, velo1, velo2 = state

    dx1dt = velo1

    dx2dt = velo2

    dv1dt = (-(stiffness1 + stiffness2) * displacement1 - 

                 (dampingCoeff1 + dampingCoeff2) * velo1 +  

                 stiffness2 * (displacement2 - displacement1) + 

                 dampingCoeff2 * (velo2 - velo1)) / mass1

    dv2dt = (stiffness2 * (displacement1 - displacement2) + 

                 dampingCoeff2 * (velo1 - velo2)) / mass2

   

    return [dx1dt, dx2dt, dv1dt, dv2dt]

# Initialising the time and creating time steps for simulation

time = np.linspace(0, 20, 2000)

 

# Initial state vector

initial_state = [displacement1_0, displacement2_0, velo1_0, velo2_0]

 

# Solve the system of ODEs

solution = odeint(TwoDOFsystem, initial_state, time)

 

# Extract the displacements of mass 1 and mass 2

displacement1 = solution[:, 0]

displacement2 = solution[:, 1]

 

# Plot the displacements

plt.figure(figsize=(10, 6))

plt.plot(time, displacement1, label='Mass 1 Displacement')

plt.plot(time, displacement2, label='Mass 2 Displacement')

plt.xlabel('Time (s)')

plt.ylabel('Displacement (m)')

plt.legend()

plt.grid(True)

plt.title('Two-Degree-of-Freedom Damped Vibration System')

plt.show()

So, let's check how the system behaves from the below plot,

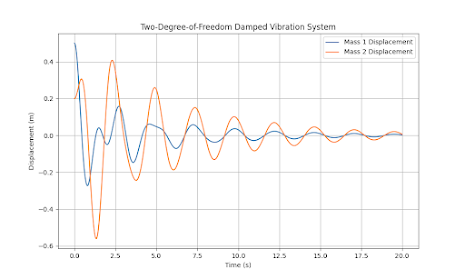
As you can see, the vibrations or displacement diminishes with time. This is because of presence of damper in the system, for each mass.

You can change the values and can play with system accordingly.

Thanks for your attention till the end. If you have any doubts or found some mistake please comment out. I will reach to you. 

If you have any topic related to mechanical field, in mind which needs some python touch please tell me, I will blog it in future.

Thank you all. See you in next blog.