Practical implications of free damped vibraton systems.

We all go through the theoretical concepts of vibrations in engineering course work and their understanding is good, but have anyone thought about their practical implications?

From the previous posts on vibration system, I have explained 1 DOF and 2 DOF free damped vibration systems. In this one, I have aimed to explain the practical implications of these free damped vibration systems.

In any vibratory system, theoretically we model the whole system using three basic elements. They are mass which provides inertia to the system, spring which helps in oscillations of the mass and damper which dampens out or reduces the oscillations of the mass. 

Now, practically, based on damping, vibratory systems are categorized into three essential concepts, namely, overdamped, underdamped and critically damped systems. Let’s check examples of each type.

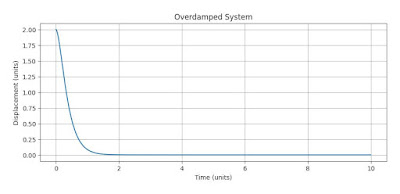
• Automatic door-closer installed in commercial buildings is an example of overdamped system. One can see that once door opens and released it doesn’t swing about the hinge of door but slowly returns to its closed position. Here, the mechanism attached to door on top side acts as damper.

Credits: https://m.indiamart.com/proddetail/aluminum-mosquito-mesh-heavy-door-with-auto-closer-24757497812.html

Figure 1. Overdamped system real life example with corresponding Time-Displacement graph.

• In park, a child’s swing oscillates back and forth, where amplitude decreases slowly over time. This is example of underdamped system where air resistance and swing joints located at top side acts as damper.  

Credits: https://lifestyle.livemint.com/relationships/raising-parents/why-your-kids-need-a-swing-set-111649308702426.html

Figure 2. Underdamped system real life example with corresponding Time-Displacement graph.

• Everyone has seen shock absorber of a bike. Whenever there is bump or pit, we didn’t experience a jerk nor do we oscillate up and down with the bike seat, instead the bike comes to original position without bouncing. This is because of shock absorber located at back side of bike. This is an example of critically damped system.

Credits: https://www.bikedekho.com/tvs/apache-160/images

Figure 3. Critically damped system real life example with corresponding Time-Displacement graph.

Let’s check the applications of damped free vibration in engineering field.

• In electronics industry, design of radio circuits is based on damped vibrations as these circuits work at specific frequencies. These are used for tuning circuits and selecting desired station among many signals.

• It is compulsory to built a earthquake-resistant buildings in earthquake prone areas. This is to prevent collapse of buildings/structures. Damped vibration system plays key role in designing these buildings, as the building itself behaves a damped system, thus resisting/storing and releasing the energies of unexpected shocks.

• In any automobile, the suspension system is designed as a damped system. It is done in order to provide stability and ride comfort. Here, the system is often critically damped.

There is a parameter called damping ratio which is used to determine how fast the oscillation of vibratory system dampens out. Well, what do you think how this is calculated and how this is related to above-mentioned examples?

Equation of motion (translational motion) for 1 DOF discrete vibrational system –

General form of equation of motion is,

ma + cv + kx = 0

The normalized homogenous second order Ordinary Differential Equation for 1 DOF discrete vibrational system is,

a + 2*zeta*v + omega^2*x = 0

Comparing both the equations we get,

zeta = c/(2m)

This zeta is called the damping ratio.

where, m ­= mass of system, 
c = damping coefficient, 
k = stiffness of system, 
a = acceleration, 
v = velocity, 
x = displacement and 
omega = angular eigenfrequency. 

Now, let’s drag the above examples here for explanation using damping ratio.

• Automatic door-closing system is an example of overdamped system, i.e., zeta > 1 or c/(2m) > 1 or, c > 2m. This tells us that the damping coefficient is greater than twice the mass. Thus, the door closes slowly without any oscillations with damping coefficient having upper hand.

• Child’s swing in the park is an example of underdamped system, i.e., zeta < 1 or c/(2m) < 1 or c < 2m. This tells us that the damping coefficient is lesser than twice of mass. Thus, the mass of the system has upper hand and therefore, oscillations are there until the swing stops. 

• Shock absorber of any automobile is an example of critical damped system, i.e., zeta = 1 or c/(2m) = 1 or c = 2m. Thus, the damping coefficient equals twice of mass. This tells us that the damper has sufficient damping coefficient to dampen out oscillations of mass and thus providing comfort ride.

 

Thanks for staying with me till the end. I hope the practical implications is now clear to you guys.

If you want other topic related to mechanical vibrations or from mechanical domain to be explained please tell me in comment section.

Thank you!!